Norman Johnson with stick and ball models.

Johnson solid 63, tridiminished icosahedron, can be constructed by 9 of 12 vertices of the regular icosahedron. The removed 3 vertices loses 15 triangular faces while adding 3 pentagonal ones. This solid appears in 4-dimension as the vertex figure of the convex uniform 4-polytope (polychoron) snub 24-cell.

Norman W. Johnson (November 12, 1930 – July 13, 2017) was a mathematician at Wheaton College, Norton, Massachusetts.

Johnson was born in Chicago. He earned his undergraduate mathematics degree in 1953 at Carleton College in Northfield, Minnesota, followed by a master's degree from the University of Pittsburgh. He earned his Ph.D. from University of Toronto in 1966 under H. S. M. Coxeter. He taught until his retirement in 1998 in the Mathematics Department of Wheaton College in Massachusetts.

Uniform polytopes

This website has been created to bring Johnson's final unpublished work, Uniform Polytopes, into public attention.

His 1966 Ph.D thesis has been uploaded here: The Theory of Uniform Polytopes and Honeycombs

Johnson's final book Geometries and Transformations was completed in 2017 just before his death and published in 2018. It was taken and expanded from introductory chapters of Uniform Polytopes.

A copy of both Uniform Polytopes and Geometries and Transformations are included below in this website.

Johnson Solids

In 1966 Johnson enumerated 92 convex non-uniform polyhedra with regular faces, now called the Johnson solids. The list was proved complete in 1969 by Victor Zalgaller. The final form listed is called a triangular hebesphenorotunda, containing 18 vertices, 36 edges, and 20 faces . It is the only Johnson solid with 3, 4, 5 and 6 sided faces (13 triangles 3 squares 3 pentagons 1 hexagon).

Uniform Polyhedra

The list of uniform polyhedra  with 75 uniform solutions with families of prism and antiprisms, were first published in 1954 by H.S.M. Coxeter (1907–2003), M.S. Longuet-Higgins, and J. C. P. Miller. The list was proved complete in 1970 by S.P. Sopov, while J. Skilling in 1975 found one more if coinciding edges are allowed.

In 1971, Johnson collaborated with teacher and polyhedral model builder Magnus Wenninger (1919–2017) in the naming of all of the uniform star polyhedra and duals, adding names for the duals in 1983.

Uniform Polychora

Between 1900 and 1912, Thorold Gosset, Alicia Boole Stott, Pieter Hendrik Schoute, and E. L. Elte began enumerating convex semiregular (archimedean) polytopes above 3 dimensions, most being related to the regular polytopes, 6 in 4-dimensions, now called the 5-cell, tesseract, 16-cell, 24-cell, 120-cell, and 600-cell. Gosset found one special form called a snub 24-cell as the truncated 24-cell with half of the vertices removed with new edges adjusted to be equal length, similar to the snub cube being a truncated cuboctahedron with half of the vertices removed.

In 1965 John Horton Conway and Michael Guy proved the complete list of uniform 4-polytopes, identifying one special case, called a grand antiprism.

Uniform polychoron project

After retirement, Johnson collaborated with amateur mathematicians including George Olshevsky (1946–2021), Jonathan Bower (1969–), Wendy Krieger and Richard Klitzing in a Uniform polychoron project to define terminology and identify and document all star uniform polytopes in 4-dimensions.

Olshevsky originally tried the name polychoremata when he publish his list of the Archimedean 4-polytopes in 1997, from Greek choros meaning "room" or "space", and Johnson suggested the shorter name polychoron. For example, the regular 5-cell can also be called a pentachoron, and an 8-cell/tesseract an octachoron.

In 2005, Johnson presented a preliminary count of 1845 uniform polychora, with the current count by Bower is 2188 and is not complete.

Scaliform polytopes (originally called weakly uniform) were identified from alternations, being vertex-transitive, with regular faces, but not all uniform cells. Cells can include Johnson solids like pyramids and cupolae.

Truncation terminology

Johnson extended Johannes Kepler's names for the Archimedean polyhedra into higher dimensions. Most of the convex uniform polytopes can be described as permutations of ringed linear Coxeter-Dynkin diagrams as Wythoffian construction. The nodes of the linear diagrams are labeled 0...n-1. Coxeter's t notation list indices for the ringed nodes.

Starting with truncation, t0,1 (cutting vertices) Johnson added cantellation t0,2 (cutting edges, Kepler's rhombi- forms), and runcination (t0,3 cutting faces). (For higher polytopes, a sterication, t0,4 cuts cells.) A uniform polychoron,t0,1,2,3, can be called an omnitruncation, or explicitly a runcicantitruncation. Deeper truncations, like t1,2 is called a bitruncation, and t1,2,3, a bicantitruncation.

Single ringed diagrams like t1 are called rectification, making new vertices on mid-edges of original polytope, and t2 is a birectification, with vertices centerd on the original faces. A dual polychoron is a trirectification, t2, with vertices centered on original cells.

Johnson followed Coxeter's snub terminology, as an alternated truncation, so Kepler's snub cube is a snub cuboctahedron, as an alternated truncated cuboctahedron.

In his PhD thesis, The Theory of Uniform Polytopes and Honeycombs, Johnson defined a new operator holosnub as a generalization of alternation, using letter eszett, ß, working across odd-order branches, retaining all vertices, but connected alternately. A  holosnubbed pentagon, ß{5} becomes a pentagram, {5/2}.

Circumradius

A finite uniform polytope has all its vertices on an n-sphere. Assuming integer edge lengths, the n-sphere radius is called the circumradius.

Vertex figures

All (finite) uniform polytopes and uniform honeycombs contain a single vertex figure type which exists in a hyperplane. (Skew regular polytopes have skew vertex figures that are not in a hyperplane.)

Regular polytopes have regular vertex figures. A regular polytope {p,q,r,s,..y,z} has facets {p,q,r,s,..y}, and vertex figures {q,r,s,..y,z}

Rectified regular polytopes have vertex figures as prism as a product of two regular polytopes, seen from the Coxeter diagram, the ringed node is removed, and adjacent nodes are ringed. For example t2{p,q,r,s} has a duoprism vertex figure {p}×{s}, while t1{p,q,r,s} has vertex figure {}×{r,s}.

Multiple ringed uniform polytopes have more complex vertex figures, but can be extracted from the Coxeter-Dykin diagram.

A dual polytope of a uniform polytope has identical facets, each facet the dual polytope of the vertex figure of the uniform

Composite polytopes

Johnson defined product, sum,  and join operators for constructing higher dimensional polytopes from lower. Johnson defines (  ) as a point (0-polytope), { } is a line segment defined between two points (1-polytope). Many vertex figures for uniform polytopes can be expressed with these operators.

A product operator, ×, defines rectangles and prisms with independent proportions. dim(A×B) = dim(A)+dim(B).

For instance { } × { } is a rectangle, symmetry [2], (a lower symmetry form of a square), and {4} × { } is a  square prism, symmetry [4,2] (a lower symmetry form of a cube), and {4} × {4} is called a duoprism in 4-dimensions, symmetry [4,2,4] (a lower symmetry form of a tesseract).

A sum operator, +, makes duals to the prisms. dim(A+B) = dim(A)+dim(B).

For instance, { } + { } is a rhombus or fusil in general, symmetry [2], {4} + { } is a square bipyramid, symmetry [4,2] (lower symmetry form of a regular octahedron), and {4} + {4} is called a duopyramid in 4-dimensions, symmetry [4,2,4] (a lower symmetry form of the 16-cell).

A join operator, v, makes pyramidal composites, orthogonal orientations with an offset direction as well, with edges between all pairs of vertices across the two. dim(AvB) = dim(A)+dim(B)+1. The isosceles triangle can be seen as ( ) v { }, symmetry [ ], and tetragonal disphenoid is { } v { }, symmetry [2].

Two further operator, , a skew-rhombic sum, and , a skew-rectangular product. dim(AB) = dim(AB) = max(dim(A),dim(B))+1. For example, {3} {3}, and  {3} {3}. {} {3} is a cube.

A final operator, atop, ||, is similar to join, except the two elements exist in the same space rather than orthogonal. In simple cases, new elements exist on a convex hull of the vertices. dim(A||B) = max(dim(A),dim(B))+1. For example, { } || { } is two parallel line segments, a square or trapezoid. And {3} || t{3} is a triangular cupola. {3} || {3} is a triangular prism, and {3} || dual {3} is a triangular antiprism.

Incidence matrices of triangles

Incidence matrices

An incidence matrix or polytope configuration is a compact description of a regular polytope, with elements ei,j and ej,i as the number of i-faces in contact with j-faces. The diagonal ei,i counts the total number of i-faces. All polytopes can be represented by incidence matrices, except there will be multiple rows and columns for each class of i-face within its symmetry.

For example, a scalene triangles has 3 types of edges a,b,c, and 3 types of vertices A,B,C, so has a 6x6 incidence matrix.

Having the incidence matrix of a polytope allows a quick summary of the number of elements with it. In practice, they become unwieldy unless a polytope has a very high symmetry.

Coxeter notation

Johnson worked with Coxeter's bracket notation for symmetry, being a symbolic form of a Coxeter-Dynkin diagram. A cube has Schlafli_symbol {4,3} with octahedral symmetry in brackets [4,3], order 48. The snub cube is sr{4,3}, and chiral octahedral symmetry [4,3]+, order 24. A regular 600-cell is also called {5,3,3} by it Schlafli symbol, and symmetry [5,3,3]. A snub 24-cell can be given different Schläfli symbols: s{3,4,3}, sr{3,3,4}, s{31,1,1}, representing symmetries [3+,4,3], [(3,3)+,4], and [31,1,1]+, order 576, 192, and 96 respectively. The + represents an alternation and cuts the symmetry order in half. The + operator can apply to portions of a Coxeter-Dynkin diagrams with all even-ordered branches. So [3+,4,3+] is an index 4 subgroup of [3,4,3], order 1152.

Johnson added a 1+ notation for removing one mirror so [1+,4,3] reduces octahedral symmetry to tetrahedral symmetry [3,3]. This is related to the alternation or half operator on polyhedra. h{4,3}, half cube is one of 2 tetrahedra. Johnson also added a * operator for radial subgroups. It removes all mirrors at a branch, so n* makes an index 2n subgroup. For example, [4,3*] ~ [2,2], removing mirrors at 3-order crossings, index 6, order 8.

The generators of a Coxeter group are the mirrors, each node. For example the affine Coxeter group [4,4] has generator mirrors {0,1,2} from its 3 nodes. The group [4,4]+ has rotational generators {01,12,02}, with two generators making the other, while [4+,4+] has generators glide reflection generators {012,120,210}, also with 2 generators making the third one.

Johnson also defined trionic operator, which reduced a symmetry by a factor of three. [3,3]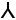 ~ [2+,4].

All of the bracket notation markups have equivant markups on the Coxeter-Dynkin diagram directly, with open nodes for alternations and gaps drawn to clarify independent alternations.

Geometries and Transfomation (2018)

  • Printed book published by Cambridge University Press
  • A searchable PDF of the chapters, no index.
    1. Homogeneous Spaces
      1. Real Metric Spaces
      2. Isometries
        • A . Isometry groups
        • B . Products of reflections
        • C. Special cases
      3. Unitary Spaces
    2. Linear Geometries
      1. Projective Planes
        • A . Incidence
        • B . Harmonic and quadrangular sets.
        • C. Order and continuity.
        • D . Coordinates.
      2. Projective n-Space
        • A . Homogeneous coordinates
        • B . Analytic proofs
        • C. Transformations
      3. Elliptic and Euclidean Geometry
      4. Hyperbolic Geometry
    3. Circular Geometries
      1. Inversive and Spherical Geometry
      2. Pseudospherical Gometry
      3. Conformal Models
        • A . Elliptic geometry
        • B . Hyperbolic geometry
        • C. Spherical and pseudospherical geometry
      4. Triangles and Trigonometry
        • A . Line segments and great arcs
        • B . Metric triangles
        • C. The Triangle Inequality
        • D . Trigonometry
      5. Non-Euclidean Circles
      6. Summary of Real Spaces
    4. Real Collinear Groups
      1. Linear Transformations
      2. Affine Collineations
      3. Homogeneous Coordinates
        • A . Assigning coordinates
        • B . Plane configurations
      4. Projective Collineations
      5. Projective Correlations
      6. Subgroups and Quotient Groups
    5. Equiareal Collineations
      1. The Real Affine Plane
      2. Ortholinear Transformations
      3. Paralinear Transformations
      4. Metalinear Transformations
      5. Summary of Equiaffinities
      6. Symplectic Geometry
        • A . Null systems
        • B . Equivalent forms
    6. Real Isometry Groups
      1. Spherical and Elliptic Isometries
        • A . Spherical isometries
        • B . Elliptic isometries
      2. Euclidean Transformations
        • A . Euclidean isometries
        • B . Similarities.
        • C. Markovian coordinates
      3. Hyperbolic Isometries
    7. Complex Spaces
      1. Antilinear Geometries
        • A . Complex projective geometry
        • B . Unitary metric spaces
      2. Anticircular Geometries
        • A . The elliptic n-antisphere
        • B . The hyperbolic n-antisphere
      3. Summary of Complex Spaces
    8. Complex Collineation groups
      1. Linear and Affine Transformations
        • A . Linear transformations
        • B . Affine transformations
      2. Projective Transform ations
      3. Antiprojective Transformations
      4. Subgroups and Quotient Groups
    9. Circularities and Concatenations
      1. The Parabolic n-Sphere
      2. The Real Inversive Sphere
        • A . Points and circles
        • B . Parabolic similarities
        • C. Reflections and inversions
        • D . Homographies and antihomographies
      3. The Complex Projective Line
      4. Inversive Unitary Geometry
    10. Unitary Isometry Groups
      1. Unitary Transformations
      2. Transunitary Transformations
      3. Pseudo-unitary Transformations
      4. Quaternions and Related Systems
        • A. Quaternionic groups
        • B. The quaternionic projective line
        • C. Clifford algebras
        • D. Octonions
    11. Finite Symmetry Groups
      1. Polytopes and Honeycombs
        • A 2-polytope is a polygon, a 3-polytope is a polyhedron, and a 4-polytope is a polychoron.
        • The vertices of a dion are its endpoints, and the edges of a polygon are its sides. The 2-faces of a polyhedron are just called faces, and the 3-faces of a polychoron are cells. The single n-face of an n-polytope is its body, essentially its “interior”; an (n-1)-face (“hyperface”) is a facet, and the (n-2)-face between two adjacent facets is a ridge.
        • An n-honeycomb, or polytopal space-filling, is abstractly the same as an (n-1)-polytope but has a scope (all or part of n-space) instead of a body. The only 0-honeycomb is an antipodation, consisting of the two points of S . A 1-honeycomb is a partition of a line or a circle, and its 1-faces are called parts. A 2-honeycomb is a tessellation of a plane or a sphere, and a 3-honeycomb is a cellulation. The n-faces (“hypercells”) of an n-honeycomb are its cellules, and the (n 1)-faces separating adjacent cellules are walls.
        • A totally ordered subset of j-faces of an n-polytope or (n-1)-honeycomb, one of each rank from 1 to n, is called a flag. A polytope or honeycomb is regular if there are isomtries permuting the vertices and taking any flag into any other flag. The nullitope ) ( is trivially regular, as are all monons ( ) and any dion { } w ith two ordinary or two absolute endpoints (but not one of each).
        • A polygon is regular if it is both equiangular and equilateral, and a partition is regular if it is equilateral. A regular p-gon, either a polygon with p vertices and p sides or a partition of the circle S into arcs of length 2pi/p, is denoted { p }. A regular apeirogon { } is either a partition of the E u clidean line E into infinitely m any equal-length segm ents or an infin ite1 polygon inscribed in a horocycle or in the absolute circle of the hyperbolic plane. A regular pseudogon {pi i/ lambda} is a partition of the hyperbolic line H1 into segments of length 2 lambda.
        • Each regular figure has a Schläfli symbol (after Ludwig Schläfli, 1814–1895). A regular polyhedron or tessellation whose face polygons are {p}’s, q meeting at each vertex, so that its “vertex figures” are {q}’s, is denoted {p,q}. In general, a regular polytope or honeycomb whose facet or cellule polytopes are {p,q,...,u}’s and whose vertex figures are {q,...,u,v}’s is denoted {p,q,...,u,v}. Each regular n-polytope P has a dual P, with the j-faces of P corresponding to the (n-j-1)-faces of P. The Schläfli symbol for P is the reverse of the symbol for P.
      2. Polygonal Groups
      3. Pyramids, Prisms, and Antiprisms
      4. Polyhedral Groups
        • TABLE 11.4. Finite Groups of Isometries in 3-Space
      5. Spherical Coxeter Groups
        • 3D
          • The irreducible spherical groups w th three generators are the full polyhedral groups A3=D3=[3,3], B3=[3,4], and H3=[3, 5] of orders 24, 48, and 120.
        • 4D
          • The groups with four generators are the full polychoric groups A4= [3,3,3], B4=[3,3,4], D4=[31,1,1], F4=[3,4,3], H4=[3,3,5] of orders 120, 192, 384, 1152, and 14400.
          • The four string diagrams represent the symmetry groups of the regular 4-polytopes, or polychora: the self-dual pentachoron (“5-cell”) {3, 3, 3}, the dual hexadecachoron (“16-cell”) {3, 3, 4} and tesseract (“hypercube”) {4, 3, 3}, the self-dual icositetrachoron (“24-cell”) {3, 4, 3}, and the dual hexacosichoron (“600-cell”) {3, 3, 5}, and dodecacontachoron (“120-cell”) {5, 3, 3}
      6. Subgroups and Extensions
        • Each Coxeter group W generated by reflections has a direct subgroup W+ generated by rotations or other direct isom etries. It m ay also have various ionic subgroups corresponding to certain subsets of the generating reflections. Such subgroups are denoted by introducing superscript plus signs in the Coxeter bracket symbol for W (cf. Coxeter & M ser 1957, pp.124–129) and can be represented graphically by replacing solid nodes in the Coxeter diagram by open nodes (Johnson & Weiss 1999a, pp. 1309–1313).
        • A. Polygonal groups
        • B. Pyramidal and prismatic groups
        • C. Polyhedral groups
        • D. Higher-dimensional groups
    12. Euclidean Symmetry Groups
      1. Frieze Patterns
        • TABLE 12.1. Two-Dimensional Frieze-Pattern Groups
      2. Lattice Patterns
        • TABLE 12.2. Two-Dimensional Lattice-Pattern Groups
      3. Apeirohedral Groups
        • TABLE 12.3. Apeirohedral Groups
      4. Torohedral Groups
        • A. Finite Euclidean planes
        • B. Finite projective planes
      5. Euclidean Coxeter Groups
      6. Other Notations
    13. Hyperbolic Coxeter Groups
      1. Pseudohedral Groups
      2. Compact Hyperbolic Groups
      3. Paracompact Groups in H3
      4. Paracompact Groups in H4 and H5
      5. Paracompact Groups in Higher Space
      6. Lorentzian Lattices
    14. Modular Transformation
      1. Real Modular Groups
      2. The Gaussian Modular Group
      3. The Eisenstein Modular Group
    15. Quaternionic Modular Groups
      1. Integral Quaternions
      2. Pseudo-Modular Groups
      3. The Hamilton Modular Group
      4. The Hurwitz Modular Group
      5. The Hybrid Modular Group
      6. Summary of Modular Groups
      7. Integral Octonions
        • A. Cayley–Graves integers
        • B. Coxeter–Dickson integers
        • C. Coupled Hurwitz integers
        • D. Compound Eisenstein integers
      8. Octonionic Modular Loops
    16. Tables
      • Table A. Real Transformation Groups
      • Table B. Groups Generated by Reflections
        1. Spherical Groups
        2. Euclidean Groups
        3. Hyperbolic Groups
    17. List of Symbols

Uniform Polytopes (final manuscript)

  • Contents coming...

References

For questions or corrections on this website, you may contact Tom Ruen, tomruen at gmail dot com.

Thank you to Roice Nelson for hosting these pages at www.roice3.org.


(Created April 10, 2022)