Elliptic

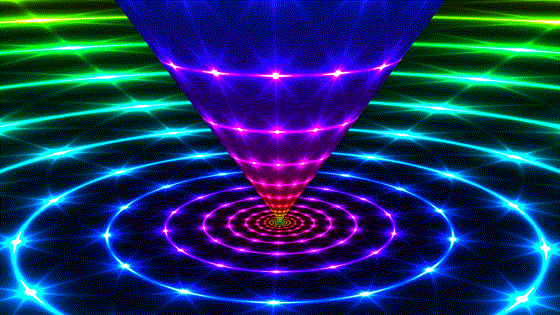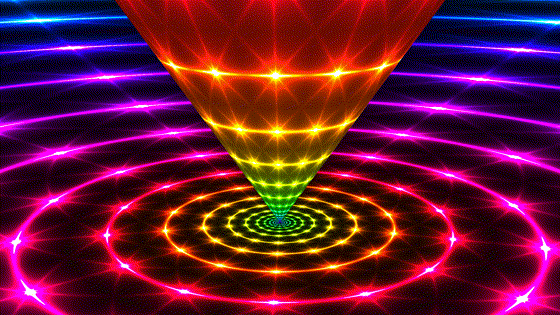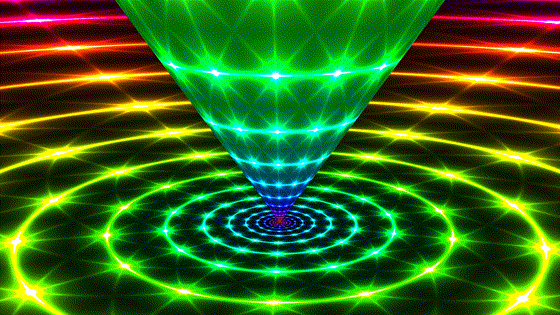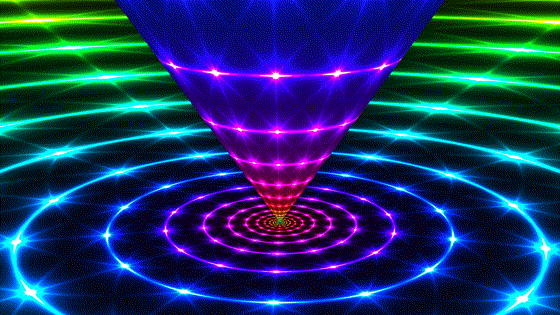
Hyperbolic


Loxodromic

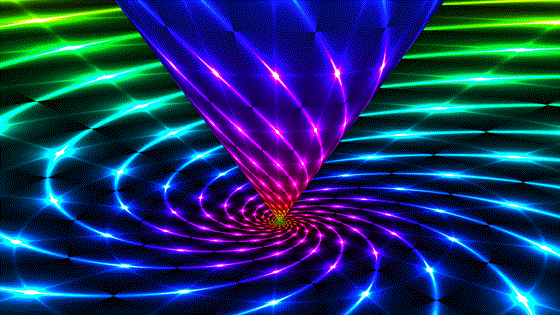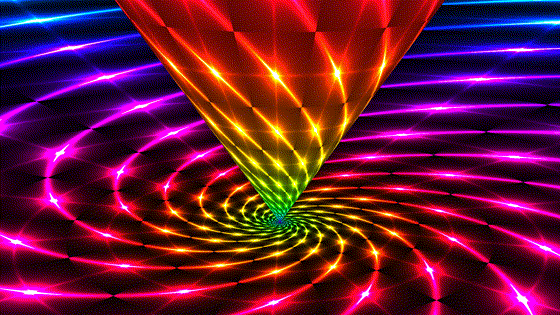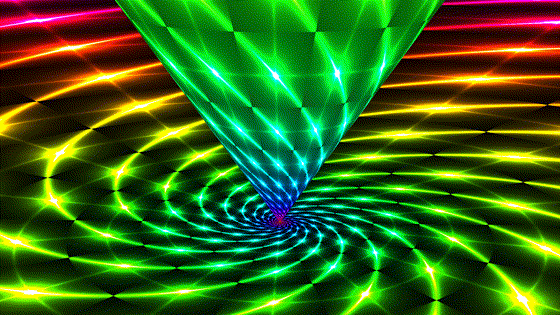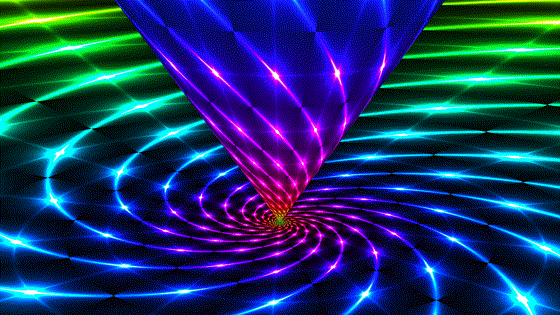
Parabolic


Here are a set of animated gifs demonstrating basic isometries (length preserving transformations) of hyperbolic 3-space, in the upper half space model.
There are four classes of transformations: elliptic, hyperbolic, loxodromic, and parabolic. These are also the classes of Möbius transformations of the complex plane. Any Möbius transformation applied to the boundary plane in the model will extend to an isometry of hyperbolic 3-space. The first three classes fix two ideal points on the boundary plane. Parabolic transformations fix just one ideal point.
You should imagine these transformations as acting on the entire upper half space, but we draw their effect on just two surfaces:
We show each transformation class in two conjugate positions. The column on the right can be considered the canonical position.
Some questions I received when posting these on social media and my answers are at the bottom. I'll gladly extend, so send comments or questions to roice3@gmail.com.
These images were all generated with a shader that you can interact with in realtime. I leveraged the python script "shadertoy-render" to capture video, and ffmpeg to turn the video into animated gifs.
Indira Chatterji turned these into lovely hand drawings.
Elliptic | |
| These are analogous to Euclidean rotations. The banana surface above the plane is a Dupin cyclide, or an inversion of a cone in a sphere, which touches the boundary at two fixed points. In hyperbolic space, this is a cylinder and points traverse parallel circles on the cylinder. An elliptic transformation is unique in that it also fixes all points along a line in the space, the core geodesic of the banana. | An elliptic with the fixed geodesic a vertical line through the origin. The surface we saw above the boundary plane is now a cone in the upper half space model (also a cylinder in hyperbolic space). The motion still fixes 2 ideal points, now at the origin and infinity. This is one of two image on this page to simultaneously show a length preserving transformation both of Euclidean space and of hyperbolic space in the upper half space model. |
 |
 |
Hyperbolic | |
| These are analogous to Euclidean translations. Points emanate from a source and disappear into a sink. The cylinder translates along its axis in hyperbolic space, while the boundary preserves a family of ideal circles sharing the 2 fixed points. | In the canonical position, it appears like we are scaling Euclidean space, but remember that the transformation depicted preserves distances in hyperbolic space! |
 |
 |
Loxodromic | |
| Loxodromic transformations are a combination of elliptic and hyperbolic, and may be more or less twisted depending on the relative contribution of each. A given point in hyperbolic space is confined to a helix on the surface of one cyclide. | In the conjugate loxodromic transformation, we see logarithmic spirals on the boundary. |
 |
 |
Parabolic | |
| Also known as "limit rotations". The sphere is a horosphere that kisses the plane at the origin, which is also the center of the horosphere and the single fixed point of the transformation. A given point in hyperbolic space is confined to a circle on one horosphere. All invariant circles of this transformation share the same ideal point. | Parabolic transformations are conjugate to translations in the model (not translations of hyperbolic space!). The fixed point is now at infinity and the plane we see is a horosphere with a center at infinity, i.e. a plane parallel to the boundary plane. It blocks our view the boundary but the pattern there is the same. This is the second image to enjoy the property that the transformation preserves Euclidean length of the model. |
 |
 |
How far out are those points at the extremities?
The two fixed points (and every point on the boundary plane in fact) are infinitely far away. They are called “ideal” points and not part of hyperbolic space.
Could you put another bean beneath?
There is a family of concentric beans (I like to call them bananas). If you added a second one in the pic, it would either be hidden inside this one or block it. You could add bananas for any other 2 ideal fixed points, but they'd be associated with a different, conjugate transformation.
Is there a transformation which turns the cone into a plane, while turning the plane it touces into a cone?
There is not. The plane is the “plane at infinity”, and all hyperbolic isometries will keep its points ideal. Likewise, the finite points on the cone will always remain finite.
Are you saying that your 3-dimensional projection makes it look like a plane and a cone?
Yes, the model necessarily warps space, analogous to how we can't represent the earth on a flat piece of paper without warping. In the space itself, that cone is actually a cylinder and the plane is the visual sphere, infinitely far away.
Lots of questions like "What is that banana-shaped blob?"
If you've made it this far, it will be easier to point you to these comments! Also, see the paper "Ortho-circles of Dupin Cyclides".
What's a good reference for hyperbolic geometry?
My intro to hyperbolic geometry came from the wonderful book Visual Complex Analysis. That introduces one to the 2-dimensional case but I always find it easiest to think in lower dimensions and then use dimensional analogy anyway.